난이도:Blonze3
문제
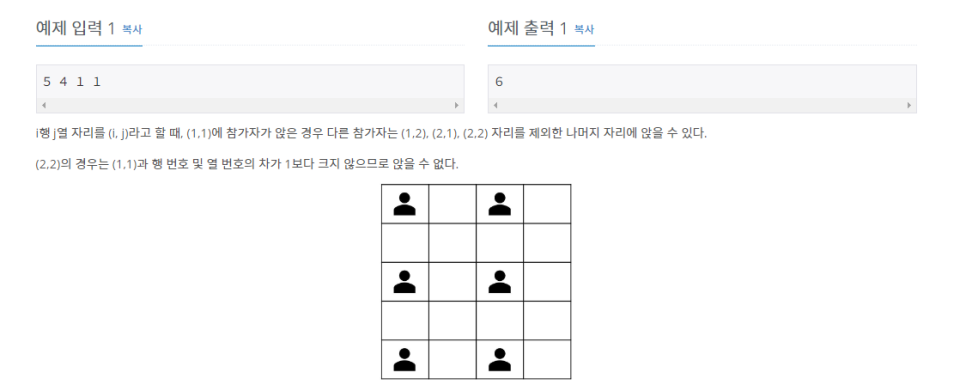
2021년 12월, 네 번째로 개최된 ZOAC의 오프닝을 맡은 성우는 오프라인 대회를 대비하여 강의실을 예약하려고 한다.
강의실에서 대회를 치르려면 거리두기 수칙을 지켜야 한다!
한 명씩 앉을 수 있는 테이블이 행마다 W개씩 H행에 걸쳐 있을 때, 모든 참가자는 세로로 N칸 또는 가로로 M칸 이상 비우고 앉아야 한다. 즉, 다른 모든 참가자와 세로줄 번호의 차가 N보다 크거나 가로줄 번호의 차가 M보다 큰 곳에만 앉을 수 있다.
논문과 과제에 시달리는 성우를 위해 강의실이 거리두기 수칙을 지키면서 최대 몇 명을 수용할 수 있는지 구해보자.
입력
H, W, N, M이 공백으로 구분되어 주어진다. (0 < H, W, N, M ≤ 50,000)
출력
강의실이 수용할 수 있는 최대 인원 수를 출력한다.
접근법
고려해야 할 점은 2가지이다.
1) 1행 1열 부터 시작 (그래야 최대 인원을 수용 가능)
2) 세로로 N칸, 가로로 M칸 떨어지기 (적게 떨어지면 거리두기가 불가능, 많게 떨어지면 최대인원이 아님)
규칙 찾기
강의실의 크기가 다음과 같이 1행에 5개의 자리가 있다고 생각해보자.
|
|
|
|
|
|
||||
1) 1칸 띄어 앉아야 할 때: 아래의 그림과 같이 3명의 인원을 최대로 수용할 수 있다.
|
1
|
x
|
2
|
x
|
3
|
||||
2) 2칸 띄어 앉아야 할 때: 2명의 인원을 수용할 수 있다.
|
1
|
x
|
x
|
2
|
x
|
||||
3) 3칸 띄어 앉아야 할 때: 2명의 인원을 수용할 수 있다.
|
1
|
x
|
x
|
x
|
2
|
||||
4) 4칸 띄어 앉아야 할 때: 더이상 인원이 들어올 수 없다.
|
1
|
x
|
x
|
x
|
x
|
||||
위의 규칙을 식으로 표현해보자.
가장 먼저 머릿속에 생각나는 식은
(강의실 크기) / (띄어앉아야 하는 칸+1) 이다.
첫번째 예시처럼 강의실 크기가 5일 때 1칸을 떨어져 앉아야 한다면 5/2, 즉 2.5가 된다.
두번째 예시처럼 2칸을 떨어져 앉아야 한다면 5/3, 즉 1.666이된다.
때문에 ceil함수를 사용하여 소수점 올림을 해주자.
가로의 최대 수용가능 인원을 구했으면, 세로도 똑같이 계산하여 준다.

이 그림을 다시한번 보자, 인원 수는 (가로 인원 수) * (세로 인원 수) 이다.
따라서 가로의 값과 세로의 값을 곱해주면 이 문제의 정답이 나온다.
정답
N, M = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(N)]
K=int(input())
for a in range(K):
sum = 0
i,j,x,y = map(int, input().split())
for b in range(i-1, x):
for c in range(j-1, y):
sum=sum+arr[b][c]
print(sum)
'Algorithm' 카테고리의 다른 글
| [백준] 2012 - 등수 매기기 (Python) (0) | 2023.03.24 |
|---|
