DQ변환의 목적
DQ 변환은 삼상 교류 신호를 회전 좌표계로 변환해 DC처럼 보이게 만들어 제어를 쉽게 하기 위함이다.
DQ 변환은 미국의 GE에서 개발되었다.
전국에서 돌아가는 3상 발전기에서 얻어진 3상 전압의 주파수, 위상, 크기 등을 동기화 해야하는데,
제어를 위해 식을 세워보니 기계시스템과 전기시스템이 결합된 비선형 상미분 3차 연립방정식이 되어버린 것이다.
제어를 할려면 이걸 적절하게 풀어내야 했다.
심지어 제어해야하는 목표전압 값도 AC 값이었다.
제어 대상이 AC면 Undamped 신호라서 2차 전달함수의 기본이론도 쓰지 못한다.
자연 주파수와 댐핑 비도 의미가 없어진다.

그래서 비선형을 최대한 선형화 하고 AC값을 DC화 할 수 있으면 좋겠다 라고 생각했다.
즉 DQ변환의 목표는 '선형화'와 'DC화' 이다.
DQ 변환은 한번에 이루어지지 않는다.
DQ변환은 2단계로 이루어진다.
첫 단계는 '120도 간격의 위상차를 가지는 abc상'을 '90도 간격의 Alpha, Beta상'으로 바꿔주는 Clarke 변환이다
.
120도 간격으로 3개의 축을 가지는 것보다는 90도로 직교하는 2개의 축을 가지고 계산하는 것이 서로 독립적이어서 계산하기가 편하기 때문이다.

3상 2극 모터의 각 abc상 권선이 놓여져있는 위치를 나타내는 것이다.
3상 모터는 공간적으로 120도 간격으로 놓여져 있는 각각의 권선(=코일)에 시간적으로 120도 간격을 가진 3상 전류를 넣어주는 것이다. 저 그림은 공간적인 분포만 의미하는 것이다.
이제 여기에 시간적으로 120도 간격인 3상 전류를 넣어주면, 아래 영상 처럼 번갈아가면서 벡터가 커지고 작아지고를 반복한다.
<5분 15초부터>
변환 방법은 아래 행렬을 계산하면 된다.

이 행렬 곱셈이 의미하는 바는 abc상의 전류값의 벡터들을 alpha축과 beta축에 각각 투영해서 더하는 것이다.
각 abc상이 alpha축 beta축에 기여하는 값이 얼만지를 하나하나 계산해서 더한다.
그러면 Alpha, Beta 평면 상에서의 벡터 크기와 위치가 어디인지를 알 수 있다.
a상이 Alpha에 기여하는 값: a상과 Alpha축은 완전히 같은 방향에 놓여있다. 즉 Cos(0)=1을 곱한다.
a상의 값은 그대로 Alpha축에 반영된다. 기하학적으로 표현하면 투영된다고 할 수 있다.
b상이 Alpha에 기여하는 값: b상은 Alpha축에서 120도만큼 반시계로 회전한 위치에 있으니 현재 b상 전류(또는 전압) 값의 Cos(120) = -1/2를 곱하면 된다.
c상이 Alpha에 기여하는 값: c상은 Alpha축에서 240도만큼 반시계로 회전한 위치에 있으니 현재 c상 전류(또는 전압) 값의 Cos(240) = -1/2를 곱하면 된다. b상과 같다.
a상이 Beta에 기여하는 값: a상과 Beta축은 직교 방향에 놓여있다. 즉 Sin(0)=0을 곱한다.
그래서 a상의 값은 Beta축에 기여하는 것이 전혀 없다. a상을 Beta축에 투영하는 것이다.
b상이 Beta에 기여하는 값: b상은 Alpha축에서 120도만큼 반시계로 회전한 위치에 있으니 현재 b상 전류(또는 전압) 값의 Sin(120) = sqrt(3)/2를 곱하면 된다.
c상이 Beta에 기여하는 값: c상은 Alpha축에서 240도만큼 반시계로 회전한 위치에 있으니 현재 c상 전류(또는 전압) 값의 Sin(240) = -sqrt(3)/2를 곱하면 된다. b상과는 부호만 다르다.

맨 앞에 2/3이 곱해지는 것은 3상을 2상으로 바꾸면서 Scale을 맞춰주기 위함이다.
이렇게 해두면 한 상당 전류가 12Arms일 때, Alpha,Beta 평면 또는 DQ 평면에서의 전류벡터 크기도
(= Sqrt(d^2+q^2) 로 구해지는 전류)도 12Arms로 동일해진다.
예를 들어, Q축 전류가 10Arms이고 D축전류가 5Arms이면 좌표변환하기 전의
현재 흐르는 상전류 값은 Sqrt(100+25) = 11.18Arms이다.

각 3상 전류에서 나오는 3개의 벡터를 직교 평면상의 1개의 벡터로 변환을 했다.
Alpha 값이 x축, Beta 값이 y축인 2차원 평면상의 2차원 벡터를 얻었다.
이제는 Alpha, Beta 전류를 얻어낸 것이다. 하지만 아직 여전히 교류(AC)값이다.
두번째 단계는 Alpha, Beta 전류를 DC값으로 바꿔주기 위해서
Direct, Quadrature축 줄여서 DQ축으로 변환하는 것이 필요하다.
여기서 Direct 축의 의미는 보통은 전기기기에서 공극 자속밀도의 값이 최대가 되는 지점을 의미한다.
Alpha, Beta 전류가 여전히 교류일 수 밖에 없는 이유는 위의 그림처럼 우리가 아직 Alpha축과 Beta축에
고정해서 머물면서 벡터가 회전하는 걸 보고 있기 때문이다.
어쩔 수 없이 하나의 전류벡터가 회전하면 그 벡터의 Alpha값은 Cos값으로 투영되니까 멀어졌다 가까워졌다 하는 것이다.
Beta값도 Sin값으로 투영되어서 Beta 축에 위치한 눈에서 가까워졌다가 멀어졌다 한다.
즉 고정좌표계에서 보고 있으면 Alpha전류도 Beta 전류도 아직 여전히 교류값이다.

그러나 그렇게 좌표변환해서 본 알파, 베타 축 전류들은 여전히 교류 파형이었다.
DQ변환의 목적은 선형화와 DC화 였으니 아직 한 단계가 더 남았다.
좌표계를 회전시키면 된다. 회전 행렬을 곱하면 좌표계가 회전을 하는 것처럼 계산된다.

이렇게 Clarke 변환한 알파베타 고정좌표계에서는 눈이 한 곳에 머물면서 벡터가 돌아가는 것을 보고 있었다면,
Park 변환한 회전좌표계에서는 눈이 회전하는 dq 회전 좌표계의 d축과 q축에 딱 붙어서 회전을 하는 것처럼 본다.
회전 변환 행렬에 보통 넣어주는 회전 값인 Theta 값을 각속도와 시간의 함수로 넣어주면 가능하다.
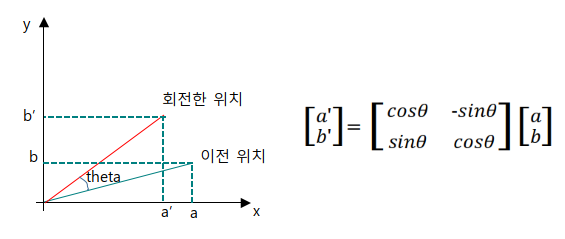
위 그림이 회전 행렬을 적용한 예시이다.
theta 만큼 반시계로 회전한 점의 위치를 찾으려면, 원래 위치에 저런 회전 변환 행렬을 곱해주면 된다.
그런데 만약에 theta 대신에 wt를 넣어준다면? (w: 각속도, t: 시간)
w의 각속도로 회전하게 된다.
그런데 그 속도를 회전하는 자기장 벡터와 같은 속도로 맞춰준다면? 즉, 전류의 주파수랑 똑같이 맞춘다면?
좌표계가 회전하는 속도가 벡터가 회전하는 속도랑 똑같아지게 된다.
그러면 좌표계에서 바라봐도 멀어졌다 가까워졌다 하지않고 일정한 거리에 있으니 일정한 값으로 보이게 된다.

이제 clarke 변환 * park 변환을 미리 곱해둔 변환행렬은 아래와 같다.


