LPF란?
Low pass filter(저주파 필터,LPF)는 말 그대로 저주파수의 신호는 통과시키고 고주파의 신호는 걸러내는 필터이다.
단어의 의미대로 해석하면 그렇지만 수학적으로 보면 고주파의 신호의 크기를 점차적으로 줄여주는 역할을 한다고 보면 된다. 주로 잡음(noise)가 고주파에 존재하기 때문에 잡음들을 제거할 때 많이 사용된다.
아날로그 LPF의 회로도는 아래와 같다. 아날로그 LPF는 지금처럼 디지털 기술이 발전하기 전, 물리적인 회로를 만들어서 신호의 잡음을 줄이기 위해 사용되었으나 현대처럼 디지털 기술이 발전한 시대에서는 아날로그보다 디지털 LPF를 사용하는 것이 편하다.
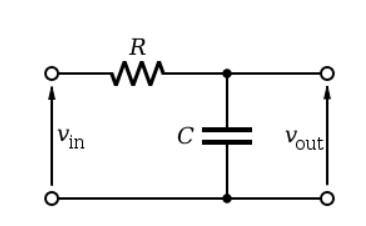
위의 LPF의 회로에서 키르히호프 법칙을 이용해 미분방정식을 새우고 라플라스 변환을 사용하여 전달함수를 구하면 아래와 같다(과정 생략).
여기서, τ는 시상수(time constant)라고 하며 τ=RC이다. 그리고 이 τ의 역수를 차단주파수(cutoff frequency, rad/s)라고 한다. 차단주파수는 LPF의 특징을 결정짓는 요소로써 통과되는 주파수 범위를 말한다.
예를 들어, 차단주파수가 10 rad/s이면 10 rad/s이하의 신호는 통과시키고 그 이상 주파수는 감소시킨다라고 이해하면 된다.
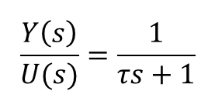
LPF는 신호의 잡음을 없애기 위해서도 많이 사용되지만 디지털 제어에서 많이 사용되며 특히, 미분기처럼 인과성(causality)이 성립되지 않는 함수를 구현할 때 많이 사용된다.
간단히 말해 출력이 입력보다 먼저 존재할 수 없다는 것이다.
예를 들어, 미분기의 전달함수를 통해 이해해보자. 미분기의 전달함수는 s이다. 미분기의 FRF(Frequency Response Function)을 보면 아래 그림처럼 표현이 된다.
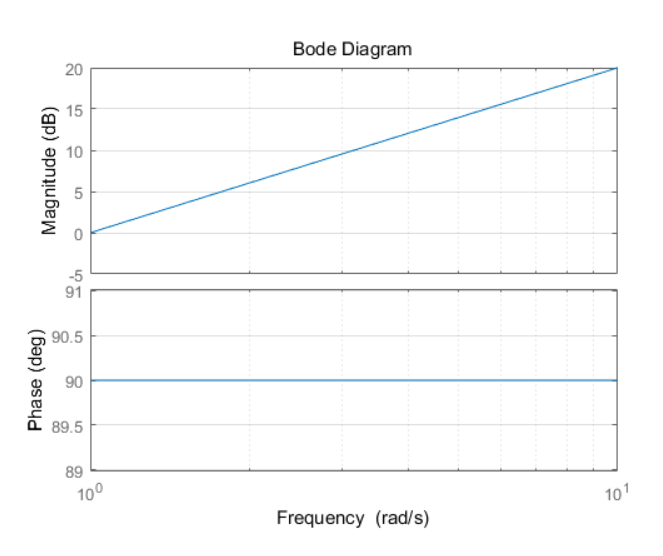
주파수 응답을 이해한 사람이라면 뭔가 이상한 점이 보일 것이다. 바로 위상(phase)부분인데, 위상이 90도라는 것은 입력 신호보다 출력신호가 1/4주기만큼 더 빨리 출력된다는 것이다. 이런 시스템은 동적 시스템의 정의에 위배되며 물리적으로 있을 수 없다(미래를 먼저 알고 있다는 의미가 된다).
미분기(s)처럼 인과성이 성립하지 않는 경우는 전달함수의 분자의 차수가 분모의 차수보다 많은 경우이다. 미분기의 차수는 1차이므로 인과성이 성립되는 미분연산을 하기 위해서는 1차 LPF를 아래 전달함수처럼 적용시켜준다.
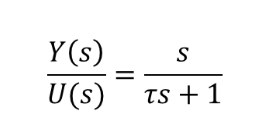
로봇공학처럼 기계시스템의 신호를 미분하는 경우(예:로봇 관절의 각속도) 신호가 대부분 저주파에 존재하기 때문에 LPF의 차단주파수를 일정이상 높게 설정하면 LPF의 영향이 적기 때문에 속도를 구할 수 있다.
차단주파수를 너무 낮게 설정해주면 딜레이가 생기고 미분된 신호도 왜곡되기 때문에 차단주파수를 목적에 맞게 잘 설정해주어야 한다.
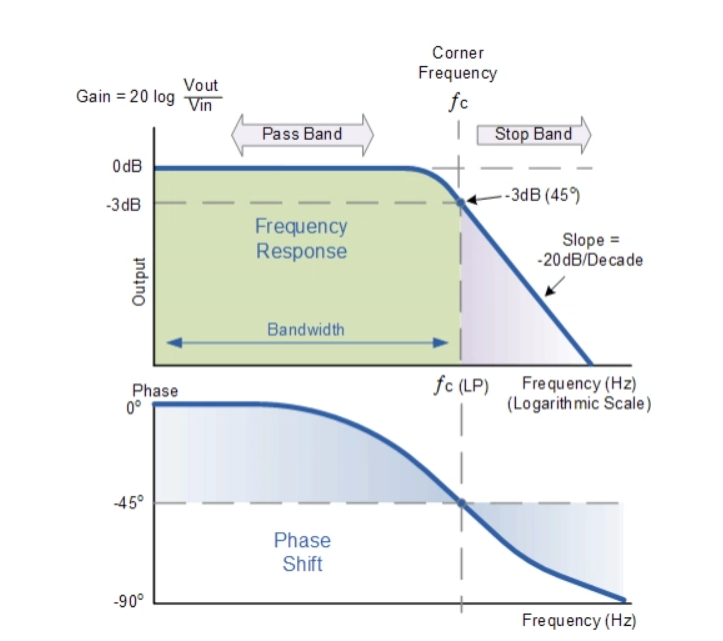
LPF의 차단주파수는 위 그림의 FRF에서 -3.01dB가 되는 지점(위상이 -45도)으로 정의되어 있는데 그 이유는 아래 수식을 보면 이해하기 쉽다. LPF의 크기를 구하기 위해 식을 풀면 아래와 같다.
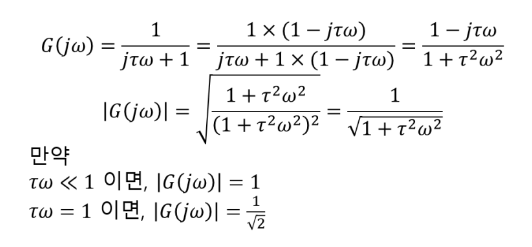
여기서 신호의 주파수가 차단주파수보다 매우 작다면 τω≪1 이므로 LPF의 크기는 1이다 (신호의 세기가 변화없이 그대로 출력). 그리고 신호의 주파수와 차단 주파수가 같게 된다면 τω=1 이 되기 때문에 크기가 약 0.707(1/√2)이 되는데 이 값을 dB단위로 바꾸면 -3.01dB이 된다. 그래서 LPF의 대역(Bandwidth)를 크기가 -3.01dB이 되는 주파수로 정의한 것이다.
참고로 2차,3차, ... n차 LPF기본형은 단순히 분모를 제곱해주면 되는데, n차 LPF는 magnitude와 phase의 형상에 따라 butter worth 필터나 chebyshev 필터처럼 여러가지 형태가 존재한다.
'인버터' 카테고리의 다른 글
| 데드타임(Dead Time) (0) | 2025.06.20 |
|---|---|
| IGBT (0) | 2024.11.14 |
| 상전압 선간전압 (2) | 2024.11.06 |
| 인버터 (3) | 2024.08.19 |